Anwendungen der Ähnlichkeit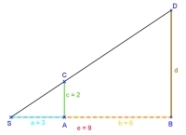
Hier gibt es neben Lehrbuchaufgaben zahlreiche interessante Links zum Thema:
Erklärt wird das Ganze in zwei PDF-Dateien (Sätze 1 bis 3 / Strahlensatz für Dummies) und auch in Videos (Film 1 / Film 2)
Übungen zur Selbstkontrolle gibt es wie so oft unter www.zum.de/dwu:
- Strahlensatz Übung 1 / Übung 2 / Übung 3
Die Uni Landau erklärt den Jakobsstab. Eine interessante Anwendung aus der Geschichte. Als Einstieg sollte man sich den Film (Menü links) und die Simulationen ansehen. Dort findet man auch ein Arbeitsheft mit Lösungen.
Auf dem Bildungsserver Baden-Württemberg findet man eine Menge Informationen und sehr gute kleine Experimente (geogebra --> Java erforderlich) zur Veranschaulichung.
Nun ein eigenes Beispiel:
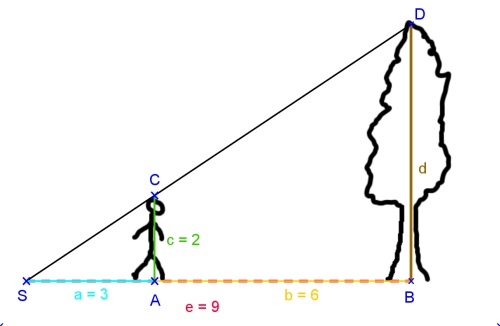
Sicher hast du dich unterwegs auch schon einmal gefragt:
Wie hoch ist der Baum?
Zum Überschlagen sei die Person 2 m groß. Solche "Riesen" soll es ja geben 
. Zum Glück scheint die Sonne und wir können die Schattenlängen a (der Person) und e (des Baumes) messen.
Jetzt wird aus der Praxis vereinfacht. Baum und "Schüler H" lassen wir einfach weg und betrachten nur noch die geometrischen Figuren (Strecken und Dreiecke). Wir nutzen die Ähnlichkeit der Dreiecke SAC und SBD. Diese stimmen im Winkel bei S und im rechten Winkel (bei A bzw. B) überein und sind nach dem Hauptähnlichkeitssatz einander ähnlich. Also stimmen die Längenverhältnisse einander entsprechender Strecken überein.
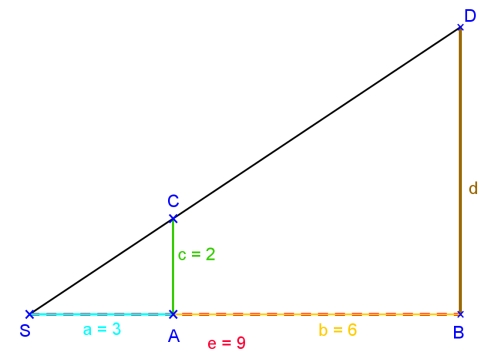
vereinfachte Abbildung: nur die Strecken sind interessant
So entsteht eine geometrische Figur, die wir später "Strahlensatzfigur" nennen können.
Nun können wir rechnen. In den beiden Dreiecken sind die einander entsprechenden Seiten a und e (Hinweis: nie später mit b verwechseln!) sowie c und d.
Also muss wegen der Ähnlichkeit gelten: "a zu e ist gleich c zu d" Da machen wir schnell eine Formel draus und rechnen.
So entsteht eine geometrische Figur, die wir später "Strahlensatzfigur" nennen können.
Nun können wir rechnen:
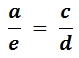Wir haben die Verhältnisgleichung aufgestellt und formen mit dem Kreuzprodukt um:
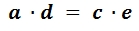Nun wird durch a geteilt, damit die Baumhöhe d allein steht:
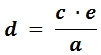In die entstandene Formel setzen wir die Werte ein:
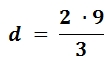Jetzt nur noch ausrechnen:
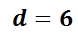
Die Baumhöhe d beträgt also 6 Meter. Wir machen noch die Probe am Sachverhalt: Die Schattenlänge des Baumes ist dreimal so lang wie der Schatten der Person. Also ist der Baum auch dreimal so hoch wie die Person. Da kann 6 Meter hinkommen.
Antwort: Der Baum ist etwa 6 Meter hoch.
War doch nicht schwer, oder? das klappt mit dem Verfahren auch mit "krummen" Zahlen und anderen Längen. So bekommt man Turmhöhen, Flussbreiten und andere Strecken im Gelände heraus, die man nicht messen kann.
Aber Achtung. Schau dir mal die Seite hier (klicken) an und vergleiche. Was ist anders? Fällt dir was auf?
